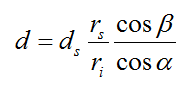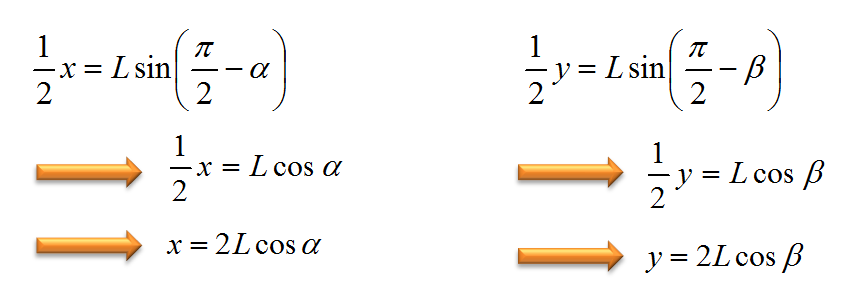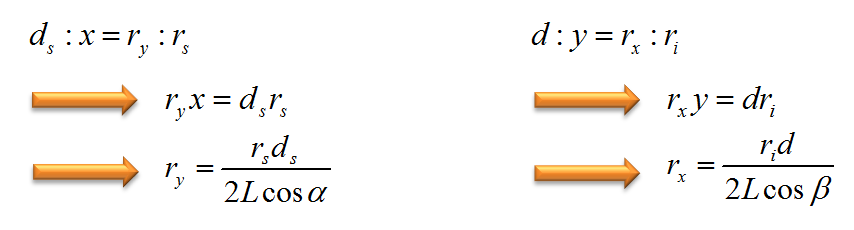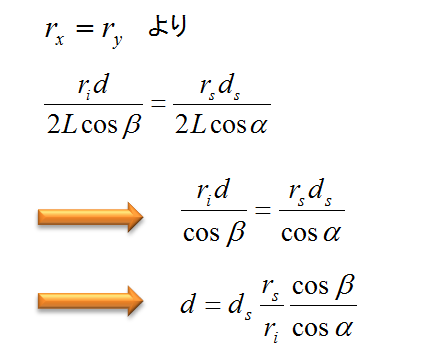わけあってXNAでPSMを実装してみました。
あと今回からファイルサイズを小さくするためにダウンロードファイルが7zip形式になっているので注意してください。

Perspective Shadow Mapsは,StammingerとDrettakisがSIGGRAPH 2002で発表したシャドウマップに関する手法です。(
論文はこちらのページ)
シャドウマップは,影を生成するための手法として,使われていますが,よく知られている問題があります。
それは,エイリアシングの問題です。Perspective Shadow Map(透視シャドウマップ)は,このエイリアシングの問題を解決するための一つの手法です。透視シャドウマップは正規化されたデバイス座標空間上で生成します。すなわち,透視変換後の空間でシャドウマップを生成するということです。さて,この様に透視変換後の空間でシャドウマップを生成すると何が良いのでしょうか?
次の図を見てください。
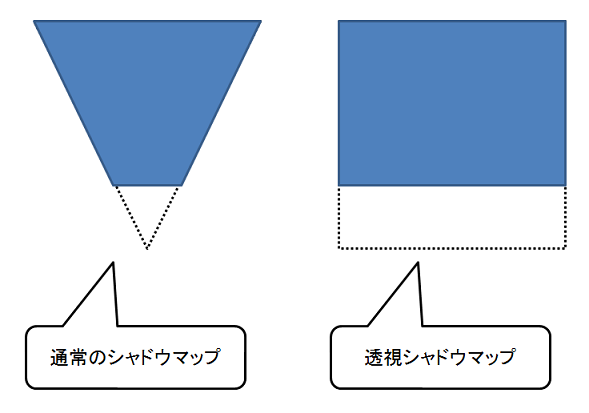
上の図は,標準のシャドウマップと透視シャドウマップの違いを示すものです。上の図に示すように通常のシャドウマップでは,錐台のような形になるのですが,透視シャドウマップでは,長方形のようにになります。透視シャドウマップは,透視投影変換してシャドウマップを生成して,視点に近い部分の解像度を高解像度にしてあげて,遠くに行くにつれてそれなりの解像度にしようというのが基本的なアイデアのようです。上の図を見ると確かに,通常のシャドウマップに比べて,カメラに近い部分の面積が大きくなっているので,高解像度で生成されそうな気がします。
まぁ,透視シャドウマップが「ある程度,使えそうだなぁ~」というのはわかるのですが,そもそも何でジャギるのかというエイリアシングの問題を理解しておかねばなりません。で,論文中にエイリアシングに関する式が載っているのですが,ずっといまいちよくわからなかったのですが,少しわかるようになったので,その説明をしておきます。
さて,エイリアシングに関してですが,まずは下の図のようにカメラを視点とした時の視野錐台とライトを視点としたときの視野錐台があるとしておきます。シャドウマップ上の各ピクセルは,このライトによる錐台を共有していることを示しており,画像空間上のds×dsのサイズのシャドウマップを通過します。
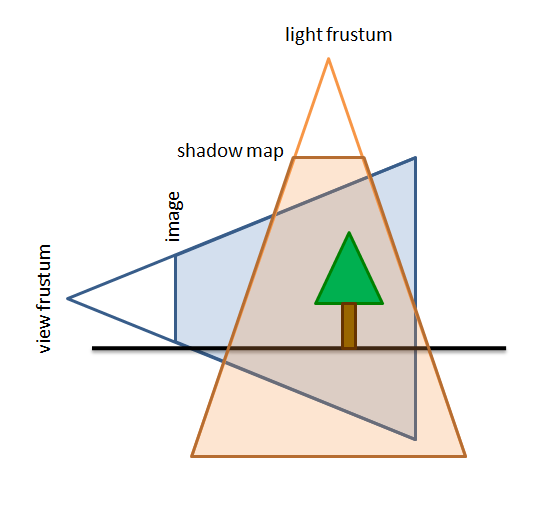
この状況のとき,下の図のようにカメラからの視線ベクトルとライトからの視線ベクトルの交差点があり,カメラから交差点までの距離をriとし,ライトから交差点までをrsとします。また,交差点での面の法線ベクトルを黒い矢印で表し,カメラの視線ベクトルと法線ベクトルのなす角をβ,ライトの視線ベクトルと法線ベクトルのなす角度をαとおきます。また,シャドウマップにぶつかったときのピクセルの一辺のサイズをds,最終的にレンダリングした結果を表示する画像平面でのピクセルの一辺のサイズをdと決めておきます。
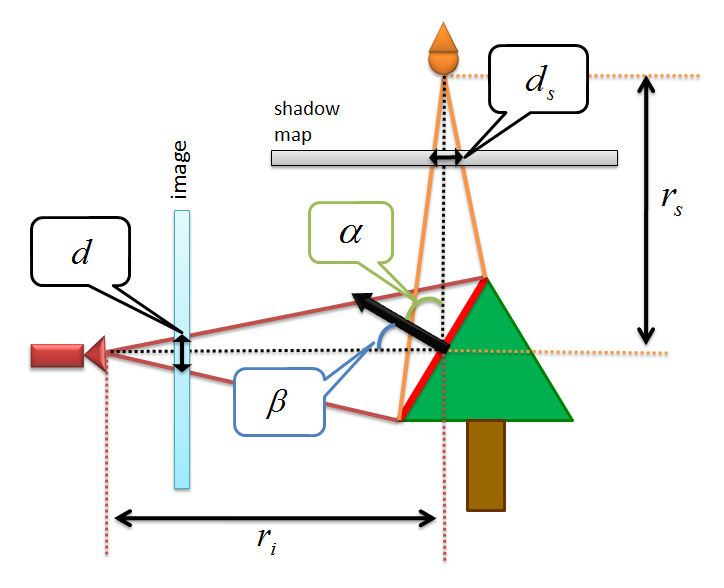
すると,画像平面上のピクセルの大きさdは次の式によって,算出されます。
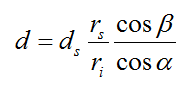
長い間,この式がどうやって算出されたのかよくわからなかったのですが,自分なりに理解できるようになったので,説明をしておこうと思います。
ちなみに,以下の説明は,間違っているかもしれません。鵜呑みにされないようにお願いします。
まず,下の図のように論文には載っていない変数x, y, rx, ryを置いておきます。あと,木は書いてあるとわかりずらいので,省略しています。
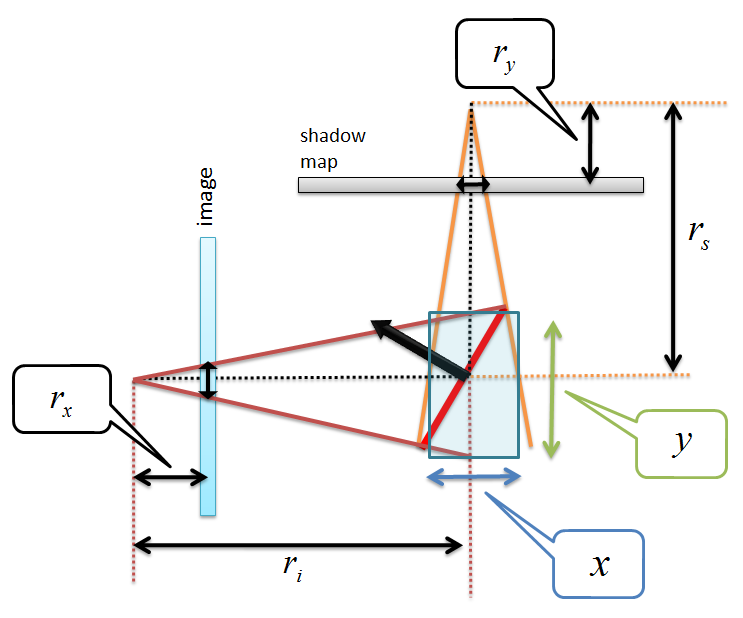
ここで,影になるギリギリの状態を考えます。影になるかどうかの判定はカメラの深度を表すriとシャドウマップに格納されている深度値rsによって決まります。よって影になるギリギリの状態はrsとriの値が一致した場合になります。すると,ニア平面とファー平面は平行になるので,ニア平面を含む三角形とファー平面を含む三角形は相似になります。よって,rsとriの値が一致するということはrxとryの値も一致するということになります。そこで,rxとryの値を求めることを考えます。
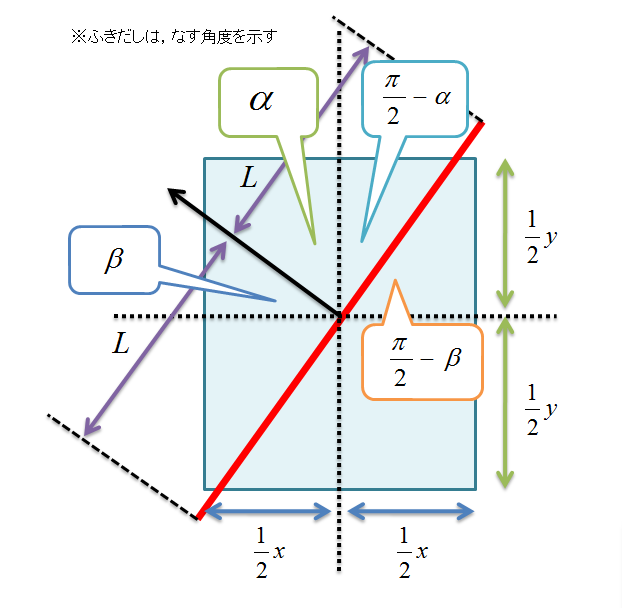
上の図は交差点の付近を拡大したものです。法線ベクトルは面となす角度が90度になるので,そこから上の図のように面とライトの視線ベクトルのなす角度が(π/2)-α,カメラの視線ベクトルと面とのなす角度が(π/2)-βと求まります。よって,この二つの角度からxとyはαとβを用いた次の式で表すことができます。
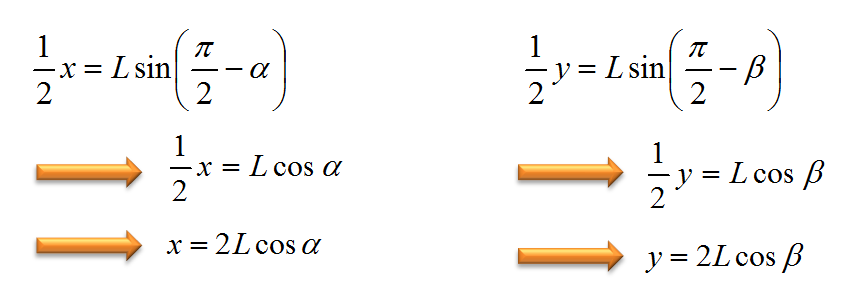
次に,先ほど述べたように,ニア平面とファー平面は平行であるので,ニア平面を含む三角形とファー平面を含む三角形は相似であることが証明できるので,次の図のように相似の関係になります。
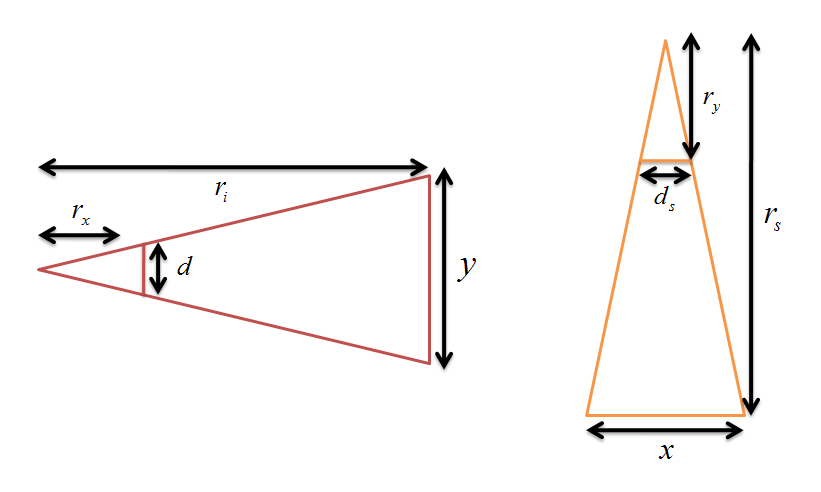
よって,相似関係から次の式が成り立ちます。
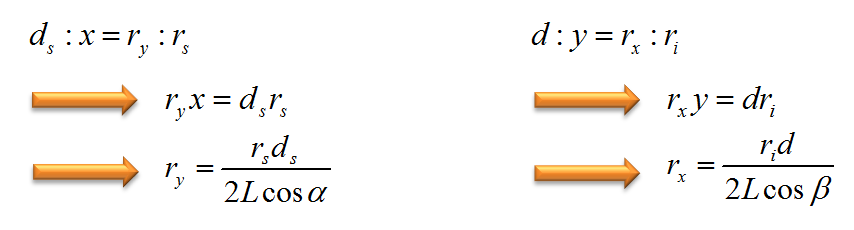
これでようやく,rxとryが表せることができました。あとは出てきたrxとryをイコールでつなげます。
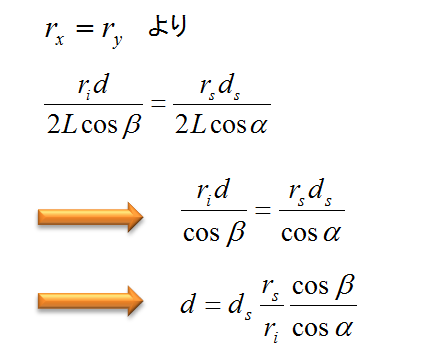
一応,自分はこんな感じで,式を導いたのですが…あっていますかね?図の作成がヘタクソなせいで,相似が成り立たなそうに見えるかもしませんが…。
まぁ,とりあえず論文中に書いてあるdを表す式があっているとしておきましょう。
大事なのは,式の意味です。まずは,directional light(方向ライト)に関して考えると,dはds*(rs/ri)に影響を受けます。シャドウマップのエイリアシングはdが画像のピクセルサイズdiより大きくなったときに発生します。つまり,ds*(rs/ri)の値が大きくなったときに,エイリアシングが発生する可能性が高まります。観測者が影の境界にズームしたときには,riの長さが小さくなるので,エイリアシングがよく発生したりするようです。論文中では,このエイリアシングのことをPerspective Aliasing(透視エイリアシング)と呼んでいます。この透視エイリアシングを避けるためには,(rs/ri)の比をある一定値に保つことで可能です。そして,これを保つには,透視変換後の空間でシャドウマップを生成すればよいと論文には書かれています。もうひとつ気をつけなければいけないのは,αとβに関してです。(cosβ/cosα)の値が大きくなったときにも透視エイリアシングが発生します。典型的な場合は,ライトの光線が地面にほぼ平行である場合です。この場合は影が地面に沿って伸びてしまいます。
さて,透視シャドウマップですが,透視変換を用いるので気をつけなくていけない点があります。例えば,次のような場合です。
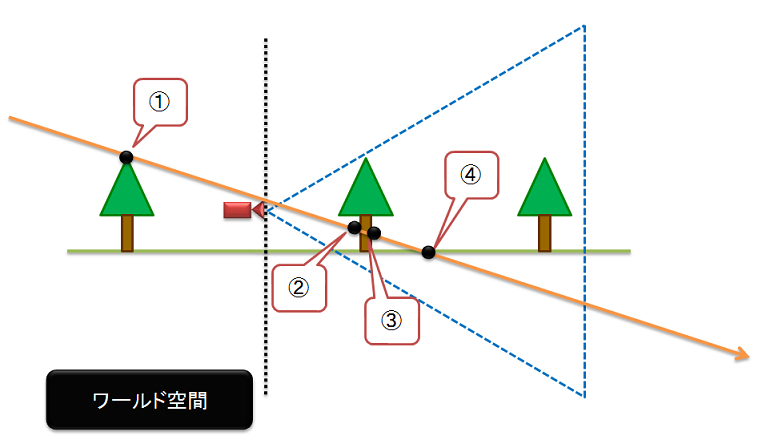
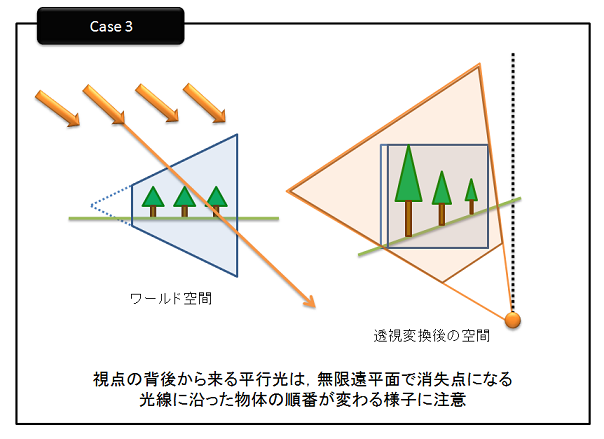
オレンジ色の線ががライトからのレイとします。すると,ワールド空間では,レイに沿って現れる点は①,②,③,④の順になります。
しかし,透視変換後の空間で考えると…
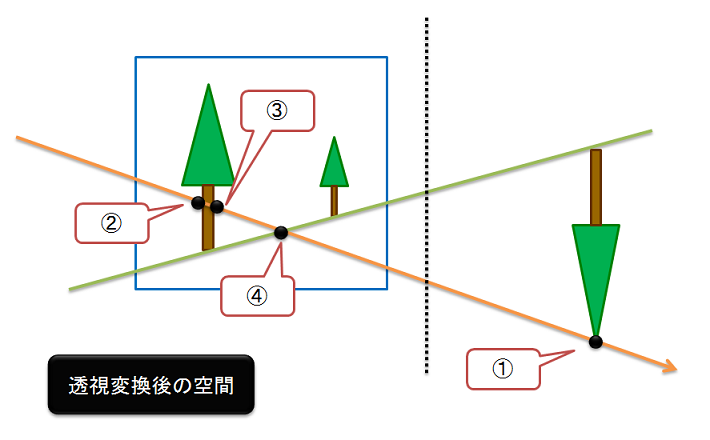
上の図のように,レイに沿って現れる点の順番は,②,③,④,①となり順序が変わってしまいます。
この問題を解決するために,論文ではカメラの後退,すなわち,シャドウマップ内に表示しなければならないシーンのすべての点が視点の前にくるまで視野錐台を後ろにするということを提案しています。確かに,このようにすればシーン内のすべての点を含むことを保証できます。
しかし,カメラを後退させると,実際にはカメラに近いオブジェクトが小さくなります。この結果,シャドウマップの使われない空間が広くなってしまうという新たな問題が発生します。この辺の透視シャドウマップの問題点については,GPU Gems 1に詳しく書いてあります。現在は,NVIDIAのサイトで英語版が読めるようになっているので,詳しく知りたい方は
こちらの文章をあたってください。
今回は,GPU Gems1に書いてあるPractical PSMの手法は使いません。
いくつか問題点があるPSMですが,実装について触れていきます。
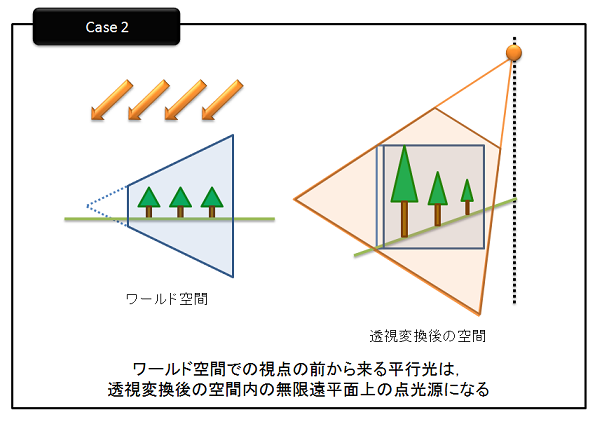
まずは,カメラ行列を用いてシーンを透視変換後の空間に変換します。このときに,変換するのに用いた行列を使ってライトも変換し,シャドウマップを生成します。このときに気をつけるのはライトは方向ライト(directional light)を使うということです。すなわち,無限遠点での点光源として考えるということです。これを実現するには同次座標系でw成分を0として取り扱えばいいことになります。さらに,気をつけてほしいのは,透視変換を用いるため,先ほど述べた順序が変化するという問題が発生する可能性があるということです。このように順序が変わってしまうのは,方向ライトが観測者の後ろにある場合です。よって,これを判定する必要があります。この判定は,単純にカメラの視線ベクトルとワールド空間での方向ライトのベクトルの内積をとれば判定できます。もし,カメラの後ろからライトが当たると判定された場合は,順序が正しくなるようにz軸に沿って視野錐台を移動させる量dz分だけ,スライドバックさせます。もちろんスライドバックさせると,ニア平面とファー平面の位置が変わってしまいますので,ニア平面とファー平面の位置が変わらないように移動量dzを足して射影行列を作成しなおします。射影行列が作成できたら,ビュー行列と掛算して,ビュー射影行列を計算します。ワールド空間の方向ライトはこの計算したビュー射影行列を使って,透視変換後の空間に変換します。行列をかけることによって,透視変換後のライトは,下の図のように点光源になる場合と,方向光源になる場合がでてきます。
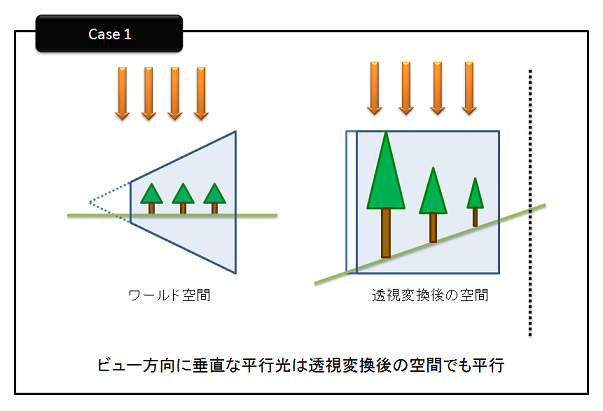
透視変換後のライトのw成分が0の場合(上図のCase 1)は平行光源(parallel light)であるので,単位キューブを包むような平行視野錐台を構築します。つまり,glOrtho()などを使ってライトの射影行列を作成します。ライトのビュー行列は透視変換後の空間なので,視点位置は(0, 0, 0)になります。注視点は,透視変換後の空間での方向ライトが見る方向になるので(-ppsLight.x, -ppsLight.y, -ppsLight.z)ただし,ppsLightは透視変換後の空間でのライトの位置とします。このパラメータによってライトのビュー行列を作成します。
透視変換後のライトのw成分が0でない場合は,光源は(ppLight.x/ppsLight.w, ppsLight.y/ppsLight.w, ppsLight.z/ppsLight.w)の有限位置にありますが,w>0である場合(上図のCase 2)は,透視変換後も光源ですが,w<0の場合(上図のCase 3)はライトの消失点になるので,zを-1倍して反転させます。そして,ライトの射影行列とライトのビュー行列を作成します。ビュー行列を作成する場合は,視点を透視変換後のライトの位置にして作成します。
ごちゃごちゃと書きましたが,最終的にシャドウマップの作成に用いる行列Mshadowは次のような形式になります。

この上の形式で書かれた行列を使ってシャドウマップを描画します。深度値の比較をするときも,この行列を用います。
コードで書くと,透視シャドウマップを作成にするのに用いる行列の求める過程は,下のようになります。
00213: /// <summary>
00214: /// PSMに用いる行列を更新する
00215: /// </summary>
00216: public void UpdateShadowMatrix()
00217: {
00218: //ワールド空間のライト
00219: Vector4 wsLight = worldSpaceLight;
00220: wsLight.Normalize();
00221:
00222: //カメラの行列を求める
00223: CalcCameraMtx(wsLight);
00224:
00225: // World Space → Post Perspective Space
00226: Vector4 ppsLight = Vector4.Transform(wsLight, viewProjection);
00227:
00228: //ライトの行列を求める
00229: if (Math.Abs(ppsLight.W) < double.Epsilon)
00230: {
00231: //平行光源の場合
00232: CalcLightMtx_ParalleLight(ppsLight);
00233: }
00234: else
00235: {
00236: //点光源の場合
00237: CalcLightMtx_PointLight(ppsLight);
00238: }
00239:
00240: //PSMに用いる行列を求める
00241: psmMatrix = viewProjection * lightViewProjection;
00242: }
おおまかな流れですが、カメラの行列を求める→ライトの行列を求める→PSMの行列を求める…といった3段階になっています。
まず最初のカメラの行列を求める処理ですが、下のような感じで求めていきます。
00244: /// <summary>
00245: /// カメラの行列を求める
00246: /// </summary>
00247: /// <param name="wsLight">ワールド空間のライト</param>
00248: void CalcCameraMtx(Vector4 wsLight)
00249: {
00250: float d = 0.0f;
00251:
00252: // Check1 : 近クリップ面までの最小距離
00253: if (nearClip < MIN_Z_NEAR)
00254: {
00255: d = MIN_Z_NEAR - nearClip;
00256: }
00257:
00258: // Check2 : Viewerの後ろから影をキャストするオブジェクトがあるか?
00259: Vector4 viewDir = new Vector4(cameraTarget - cameraPosition, 0.0f);
00260: viewDir.Normalize();
00261:
00262: //ライトと視線ベクトルのなす角を算出
00263: float dot = Vector4.Dot(wsLight, viewDir);
00264:
00265: //カメラの後ろからライトが当たるか判定
00266: if (dot < 0.0f && (float)Math.Abs(wsLight.Y) > float.Epsilon)
00267: {
00268: float t = -(MAX_Y_SCENE - cameraPosition.Y) / wsLight.Y;
00269: d = Math.Max(d, t * (float)Math.Sqrt(wsLight.X * wsLight.X + wsLight.Z * wsLight.Z));
00270: }
00271:
00272: //ビュー行列・射影行列を作成
00273: view = Matrix.CreateLookAt(cameraPosition, cameraTarget, cameraUpVector);
00274: projection = Matrix.CreatePerspectiveFieldOfView(fieldOfView, aspectRatio, nearClip, farClip);
00275:
00276: //視錐台の調整が必要か判定
00277: if (d > 0.0f)
00278: {
00279: //z軸に沿ってスライドバック
00280: view.M43 -= d;
00281: projection = Matrix.CreatePerspectiveFieldOfView(fieldOfView, aspectRatio, nearClip + d, farClip + d);
00282: }
00283:
00284: //ビュー射影行列を作成
00285: viewProjection = view * projection;
00286: }
続いて、ライトの行列を求める処理ですが、平行光源と点光源の場合で処理を分けています。
00288: /// <summary>
00289: /// 平行光源の場合のライトの行列を求める
00290: /// </summary>
00291: /// <param name="ppsLight">透視変換後の空間のライト</param>
00292: void CalcLightMtx_ParalleLight(Vector4 ppsLight)
00293: {
00294: lightView = Matrix.CreateLookAt(Vector3.Zero, ToVector3(ppsLight), Vector3.UnitZ);
00295: lightProjection = Matrix.CreatePerspectiveOffCenter(-SQRT2, SQRT2, -SQRT2, SQRT2, -SQRT2, SQRT2);
00296:
00297: //ライトのビュー射影行列を作成
00298: lightViewProjection = lightView * lightProjection;
00299: }
00300:
00301: /// <summary>
00302: /// 点光源の場合のライトの行列を求める
00303: /// </summary>
00304: /// <param name="ppsLight">透視変換後の空間のライト</param>
00305: void CalcLightMtx_PointLight(Vector4 ppsLight)
00306: {
00307: //ブラックホールかどうかチェック
00308: if (ppsLight.W < 0.0f)
00309: {
00310: //マイナスをかけて反転させる
00311: Matrix scale = Matrix.CreateScale(1.0f, 1.0f, -1.0f);
00312: ppsLight = Vector4.Transform(ppsLight, scale);
00313: }
00314: //W成分で割って変換
00315: ppsLight *= (1.0f / ppsLight.W);
00316: ppsLight.W = 0.0f;
00317:
00318: //ライトの視錐台を調整
00319: float radius = SQRT3;
00320: float dist = ppsLight.Length();
00321: float fov = 2.0f * (float)Math.Atan(radius / dist);
00322: float nearDist = Math.Max(dist - radius, 0.0001f);
00323: float farDist = dist + radius;
00324:
00325: //ライトのビュー行列・射影行列を作成
00326: lightView = Matrix.CreateLookAt(ToVector3(ppsLight), Vector3.Zero, Vector3.UnitZ);
00327: lightProjection = Matrix.CreatePerspectiveFieldOfView(fov, 1.0f, nearDist, farDist);
00328:
00329: //ライトのビュー射影行列を作成
00330: lightViewProjection = lightView * lightProjection;
00331: }
00332:
上のような感じで、コードを書けばPSMは実装できるのですが…
いかんせん使い勝手がよろしくなく、パラメータ調整が面倒です。
もう少し使い勝手がいいものを、実装中なのですが…
うまくいっておりません!
そんなわけで「PSMはちゃんと実装できていたよな?」というのを確認するために、XNAでPSMを実装したのでありました。
本ソースコードおよびプログラムを使用したことによる如何なる損害も製作者は責任を負いません。
本ソースコードおよびプログラムは自己責任でご使用ください。
プログラムの作成にはMicrosoft Visual Studio 2008 SP1 Professional,およびXNA Game Studio 3.1を用いています。