布のシミュレーション

　今回はバネのシミュレーションの応用ということで，布のシミュレーションです。
※もうちょいそれっぽく見えるようにパラメータを調節しました。(2007/11/15)

　布っぽく見せるためには，布の性質である「編まれた方向に伸びにくい」「せん断に対して伸びやすい」「非常に曲がりやすい」という性質を再現しないといけないそうです。
この性質を質点バネモデルで表現する場合には，Stretch（引っ張りに対して抵抗する接続),Shear（せん断に対して抵抗する接続）, Bending（曲げに対して抵抗する接続）を持たせてそれぞれのバネ定数を各接続の性質を再現するように適切に設定します。
質点にかかる力は…

F = Stretch + Shear + Bending

によって求められるそうです。
で，バネを接続するのに有名なやつに「Landerモデル」と「Choiモデル」っていうのがあるそうです。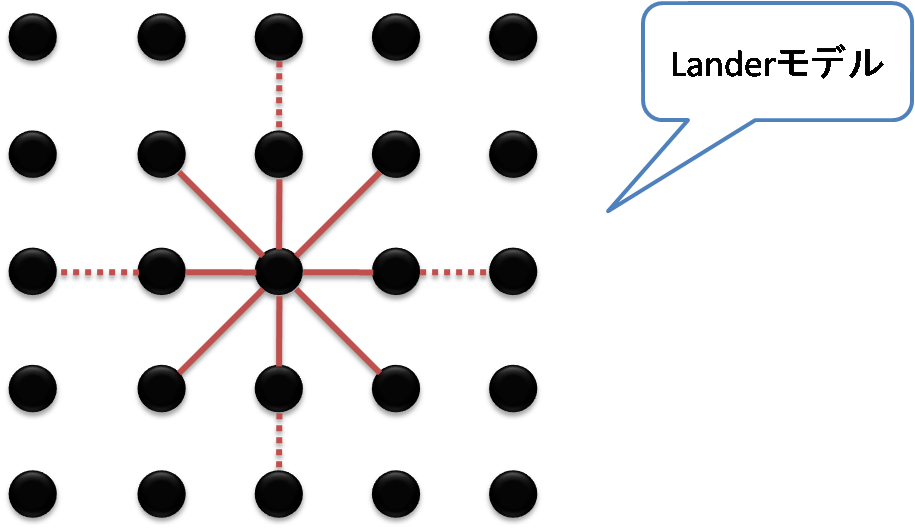


↑Landerモデル


↑Choiモデル

布関連の研究については，あまり詳しくないのですが，Choiのモデルの方が多いのかな？（違うかもしれないけど…）
上のようにLanderモデルは
(1)「上」「下」「左」「右」
(2)「左上」「右上」「左下」「右下」
(3)「一つ飛ばしの上」「一つ飛ばしの下」「一つ飛ばしの左」「一つ飛ばしの右」
を接続するそうです。

一方，Choiモデルは
(1)「上」「下」「左」「右」
(2)「左上」「右上」「左下」「右下」
(3)「一つ飛ばしの上」「一つ飛ばしの下」「一つ飛ばしの左」「一つ飛ばしの右」「一つ飛ばしの左上」「一つ飛ばしの右上」「一つ飛ばしの左下」「一つ飛ばしの右下」
を接続するそうです。

論文によるとバネの強さは(1)＞(2)＞＝(3)といった風にするようです。
最低限(1)と(2)の接続さえしておけば布っぽく見えるそうです。 それっぽく見えればよいので，プログラムでは(1)と(2)の接続のみ用いることにしました。ちなみに(3)の接続に用いるバネはフックの法則に従わないバネを想定しているそうな…
バネを接続したら前回のバネのシミュレーションのようにオイラー法を使って計算すればよいのですが，前回書くの忘れたんですが一応物理シミュレーションやっているので，エネルギー保存則が成立します。つまり，このままではエネルギー保存則により永遠に振動するバネができてしまいます。当然，我々が住む世界にそんな布があったら怖すぎるので，振動を止めなくちゃいけません。
そこで，空気抵抗を導入します。高校の物理でもやるように空気抵抗は速度の逆向きに働く力とします。

F = - d * v

ただし，F:空気抵抗，d：ダンパ定数, v：速度　とします。

この空気抵抗を導入して，あとは各格子点ごとにその格子点に働く合力を求めて，そこからオイラー法で計算すれば，シミュレーションが動くと思います。

次のようにプログラムを組んでみました。

struct Grid
{
    double mass;
    vector3d position;
    vector3d velocity;
    vector3d force;

    Grid()
    {
        position.Zero();
        velocity.Zero();
        force.Zero();
    }
};

typedef vector<vector<Grid>> Grids;

class Cloth
{
public:
    Cloth();
    ~Cloth();
    void Initialize();
    void LoadTexture(const char *filename);
    void Update();
    void Render();
    const Grid& GetGrid(int x, int y) const { return grids[x][y]; }

protected:
    void UpdateForce();
    void EularMethod();
    DDSImage texture;

    Grids grids;
    int counter;

};

各格子点に対応するのがGridクラスです。位置と速度と力を変数として持たせます。
各格子点をバネで接続して布をシミュレーションするのがClothクラスです。ベクターコンテナでGridクラスを二次元配列化したGridsクラスを持たせます。

//-----------------------------------------------------------------------------------------------------
//　　UpDateForce
//　　Desc : 力の更新
//-----------------------------------------------------------------------------------------------------
void Cloth::UpdateForce()
{
    for ( int j=0; j<NumGrid; j++ )
    {
        for ( int i=0; i<NumGrid; i++ )
        {
            if ( ( i == 0 && j == (NumGrid-1) ) || ( i == (NumGrid-1) && j == (NumGrid-1)) )
                continue;

            Grid &g = grids[j][i];

            ///　1つのグリッドに働く合力を求める　///

            //　力をゼロにする
            g.force.Zero();
            
            //　重力
            g.force.y -= g.mass * gravity;

            //　風
            double r1 = counter/70.0;       
            double r2 = counter/25.0;
            g.force.z += ( (sin(r1)*sin(r2) * 0.5 + 0.5 + 0.5) * windforce );
            
            //　ダンピング
            g.force -= g.velocity * damping;

            //　上のバネ
            if ( j <= NumGrid - 2)
            {
                vector3d d = g.position - grids[j+1][i].position;
                vector3d n = d.UnitVector();
                g.force += n * ( (spring_length - d.Length() ) * k );
            }

            //　下のバネ
            if ( j >= 1 )
            {
                vector3d d = g.position - grids[j-1][i].position;
                vector3d n = d.UnitVector();
                g.force += n * ( (spring_length - d.Length() ) * k );
            }

            //　左のバネ
            if ( i >= 1 )
            {
                vector3d d = g.position - grids[j][i-1].position;
                vector3d n = d.UnitVector();
                g.force += n * ( ( spring_length - d.Length() ) * k );
            }

            //　右のバネ
            if ( i <= NumGrid -2 )
            {
                vector3d d = g.position - grids[j][i+1].position;
                vector3d n = d.UnitVector();
                g.force += n * ( ( spring_length - d.Length() ) * k );
            }

            //　左上のバネ
            if ( i >= 1 && j <= NumGrid -2 )
            {
                vector3d d = g.position - grids[j+1][i-1].position;
                vector3d n = d.UnitVector();
                g.force += n * ( ( d_spring_length - d.Length() ) * kd );
            }

            //　右上のバネ
            if ( i <= NumGrid - 2 && j <= NumGrid -2 )
            {
                vector3d d = g.position - grids[j+1][i+1].position;
                vector3d n = d.UnitVector();
                g.force += n * ( ( d_spring_length - d.Length() ) * kd );
            }

            //　左下のバネ
            if ( i >= 1 && j >= 1 )
            {
                vector3d d = g.position - grids[j-1][i-1].position;
                vector3d n = d.UnitVector();
                g.force += n * ( (d_spring_length - d.Length() ) * kd );
            }

            //　右下のバネ
            if ( i <= NumGrid -2 && j >= 1 )
            {
                vector3d d = g.position - grids[j-1][i+1].position;
                vector3d n = d.UnitVector();
                g.force += n * ( (d_spring_length - d.Length() )* kd );
            }
        }
    }

}

下から順に格子を組んでいて，一番左上の点と一番右上の点は固定点とするので，for文の始めでif文により固定点かどうかをチェックします。固定点であった場合は力の計算はcontinue文で処理しないようにします。
あとは，格子点に働く合力を求めていきます。
まず，重力が働くのでg.force.yに重力を加算します。つぎに，これだけだと面白くないので，風力としてz方向に適当に決めた力をかけます。
次に，ダンパの力を求めて加算し，バネによる力を求めていきます。
バネによる力は位置座標から，方向ベクトルを計算し，その方向ベクトルを正規化したものに計算により求めた力の大きさに掛けてやれば求まります。

本ソースコードおよびプログラムを使用したことによる如何なる損害も製作者は責任を負いません。
本ソースコードおよびプログラムは自己責任でご使用ください。
プログラムの作成にはMicrofost Visual Studio 2005 Professionalを用いています。

• ClothSimulation.lzh (50KB)