
バネのシミュレーション
★ 1.はじめに
布のシミュレーションをやってみたかったので,今回はその下準備として1次元のシンプルなバネのシミュレーションをやってみます。


★ 2.物理計算
バネのシミュレーションを行うには重りの位置を物理計算によって求めることが必要となります。
では,どうやって重りの位置を求めればよいでしょうか?重りの位置を求めるために次の関係を利用します。
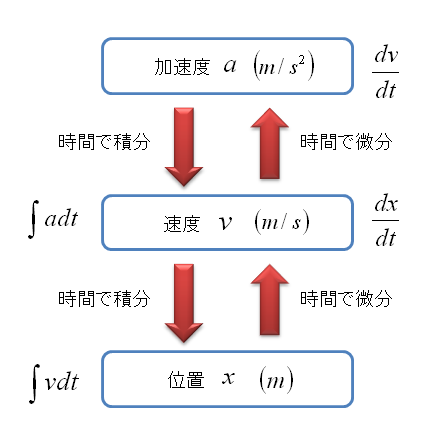
加速度がわかれば,それを時間で積分することによって速度が求められます。さらに速度を時間で積分することによって位置が求められます。
よって,運動方程式により,まず加速度を求めます。つぎに時間で積分して速度を求め,さらに時間で積分して位置を求め,もとめた位置をOpenGLで表示しれやればいいということになります。
まずは,バネにおもりをつけた時の運動方程式を考えてみます。
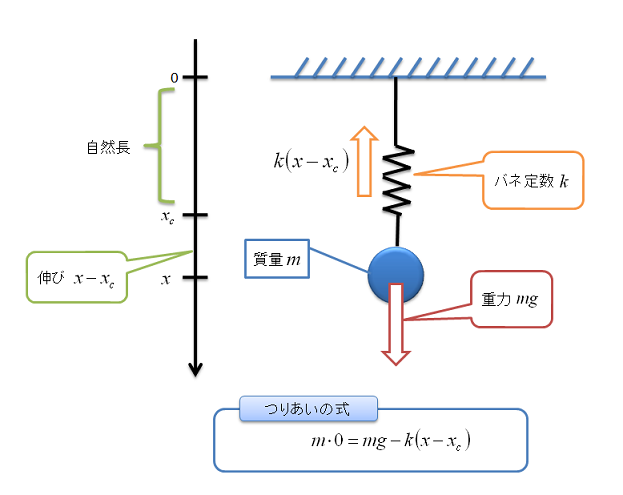
重りの質量をm,バネ定数をk,自然長をxc,現在の位置をxとすると重りにかかる力は上のような関係になります。
ここでは鉛直下向きを正の値としています。
運動方程式を立てると,現在釣り合っているので,加速度は0で,かかっている力は重力とバネによる力のみなので,上のようにm・0=mg-k(x-xc)という風になります。
もし,バネが動いているとしたら,つりあいの式の左辺のm・0がm・aになります。
ここでma=mg-k(x-xc)という式を加速度aについて解いてみると下のような式になります。
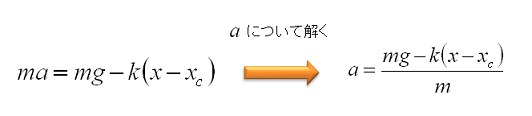
これで加速度が求められました。あとはこれを時間で積分すればよいのですが…これをプログラム上でやるには少々むずかしい気がします。
そこで厳密に積分計算をするという方法ではなく,近似的に積分計算をして解くという方法を利用することにします。
近似的に解く方法は色々とあるのですが,ここでは一番シンプルであると思われるオイラー法を利用してみます。
ある値を微小量で割ったのが微分です。微分と積分は互いに逆演算であるので,ある値に微小量を掛けたのが積分という風にも解釈できます。よって,運動方程式により求めた加速度に微小時間を掛ければ,微小時間たったときの速度がわかります。さらに速度に微小時間をかければ微小時間たったときの位置がもとめられます。これがオイラー法の直観的説明です。
もうちょっとだけ踏み込んだ説明をすると…

位置を時間で微分すると速度がでます。そのときのdx/dt=v(t)を微分の定義式よって書くと上の図の一番上の式になります。ここでΔtが十分小さいと仮定します。するとこのv(t)の式は(x(t+Δt)-x(t))/Δtという風に近似できます。ここで,この式をx(t+Δt)について解くとx(t+Δt)=x(t)+v(t)Δtという風に変形することができます。
つまり,ひとつ前の時刻tにおける位置にひとつ前の時刻tにおける速度に微小時間Δtを掛けたものを足すと次の時刻t+Δtにおける位置がわかるということになります。
位置で計算しましたが,速度でも同様にしてできます。
よってオイラー法で計算するときはつぎの式を利用すればいいということになります。
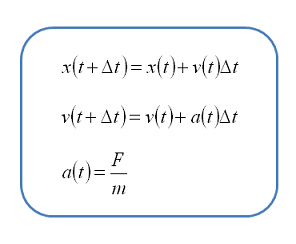
あとはさっき絵を描いてもとめた加速度をつかって上のオイラー法の式に放り込んでやればバネのシミュレーションができます。
ここで気をつけてほしいのは,Δtが十分に小さいときにオイラー法が使えるということです。Δtが大きい場合にはシュミレーションが発散したりしてしまうので気をつけてください。
プログラムで書くと下のような感じになります。
では,どうやって重りの位置を求めればよいでしょうか?重りの位置を求めるために次の関係を利用します。

加速度がわかれば,それを時間で積分することによって速度が求められます。さらに速度を時間で積分することによって位置が求められます。
よって,運動方程式により,まず加速度を求めます。つぎに時間で積分して速度を求め,さらに時間で積分して位置を求め,もとめた位置をOpenGLで表示しれやればいいということになります。
まずは,バネにおもりをつけた時の運動方程式を考えてみます。

重りの質量をm,バネ定数をk,自然長をxc,現在の位置をxとすると重りにかかる力は上のような関係になります。
ここでは鉛直下向きを正の値としています。
運動方程式を立てると,現在釣り合っているので,加速度は0で,かかっている力は重力とバネによる力のみなので,上のようにm・0=mg-k(x-xc)という風になります。
もし,バネが動いているとしたら,つりあいの式の左辺のm・0がm・aになります。
ここでma=mg-k(x-xc)という式を加速度aについて解いてみると下のような式になります。

これで加速度が求められました。あとはこれを時間で積分すればよいのですが…これをプログラム上でやるには少々むずかしい気がします。
そこで厳密に積分計算をするという方法ではなく,近似的に積分計算をして解くという方法を利用することにします。
近似的に解く方法は色々とあるのですが,ここでは一番シンプルであると思われるオイラー法を利用してみます。
ある値を微小量で割ったのが微分です。微分と積分は互いに逆演算であるので,ある値に微小量を掛けたのが積分という風にも解釈できます。よって,運動方程式により求めた加速度に微小時間を掛ければ,微小時間たったときの速度がわかります。さらに速度に微小時間をかければ微小時間たったときの位置がもとめられます。これがオイラー法の直観的説明です。
もうちょっとだけ踏み込んだ説明をすると…

位置を時間で微分すると速度がでます。そのときのdx/dt=v(t)を微分の定義式よって書くと上の図の一番上の式になります。ここでΔtが十分小さいと仮定します。するとこのv(t)の式は(x(t+Δt)-x(t))/Δtという風に近似できます。ここで,この式をx(t+Δt)について解くとx(t+Δt)=x(t)+v(t)Δtという風に変形することができます。
つまり,ひとつ前の時刻tにおける位置にひとつ前の時刻tにおける速度に微小時間Δtを掛けたものを足すと次の時刻t+Δtにおける位置がわかるということになります。
位置で計算しましたが,速度でも同様にしてできます。
よってオイラー法で計算するときはつぎの式を利用すればいいということになります。
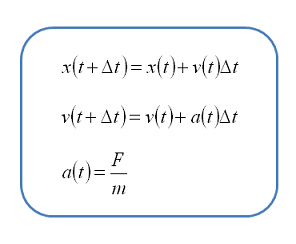
あとはさっき絵を描いてもとめた加速度をつかって上のオイラー法の式に放り込んでやればバネのシミュレーションができます。
ここで気をつけてほしいのは,Δtが十分に小さいときにオイラー法が使えるということです。Δtが大きい場合にはシュミレーションが発散したりしてしまうので気をつけてください。
プログラムで書くと下のような感じになります。
const double mass = 1.0; // 質量
const double gravity = 9.80665; // 重力加速度
const double dt = 0.01; // 微小時間
const double k = 100.0; // ばね定数
const double natural_length = 0.0; // 自然長
const double first_accel = gravity; // 初期加速度
const double first_velocity = 10.0; // 初期速度
const double first_position = 10.0; // 初期位置
double position = first_position; // 位置
double velocity = first_velocity; // 速度
double accel = first_accel; // 加速度
//------------------------------------------------------------
// Euler_Method
// Desc : オイラー法により位置を算出
//------------------------------------------------------------
void Euler_Method()
{
double force = 0.0;
// 力を求める
force = -k*(position - natural_length) + mass * gravity;
// 加速度を求める
accel = force / mass;
// 速度を求める
velocity += accel * dt;
// 位置を求める
position += velocity * dt;
}
★ Download
本ソースコードおよびプログラムを使用したことによる如何なる損害も製作者は責任を負いません。
本ソースコードおよびプログラムは自己責任でご使用ください。
プログラムの作成にはMicrosoft Visual Studio 2005 Professional Editionを用いています。
本ソースコードおよびプログラムは自己責任でご使用ください。
プログラムの作成にはMicrosoft Visual Studio 2005 Professional Editionを用いています。