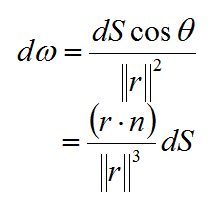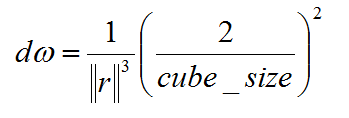球面調和関数を使ってキューブマップを近似してみました。
下の図はかなり手抜きアリアリで適当に作ってます。

SHを5次まで計算して,圧縮画像が出力されるようにプログラムを作りました。
下図は,元画像と球面調和関数を使って近似した画像を比較したものです。


最初のセットが
Paul Debevecさんのとこから持ってきた画像で,次のセットは以前XNAのサンプルで使ったことのあるTerragen使って作った画像です。
さて,近似データの作成ですが…それほど難しくはありません。
SH投影して,球面調和関数のスケーリング係数を求めます。あとはこの求まったスケーリング係数を使って球面調和関数の値をスケーリング倍して,足し合わせてやれば近似できます。トライゼットの西川さんが書かれている記事に説明があるので
【コラム】3Dグラフィックス・マニアックス(68)事前計算放射輝度伝搬(PRT)〜PRTの基本。静的PRT(3)を参照してください。
スケーリング係数の求め方については,上記ページだとほとんど触れられていないので,こちらについては触れておきます。
スケーリング係数を求める式は下記のようになります。
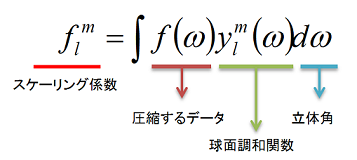
圧縮するキューブマップの各ピクセルの値に球面調和関数と立体角をそれぞれ掛け合わして,足してやればスケーリング係数が求まります。ピクセルの値と球面調和関数の値については問題ないでしょう。つまづくとすれば立体角です。
立体角は下記のような式で求まるそうです…。(
物理のかぎしっぽさんのページ参照)
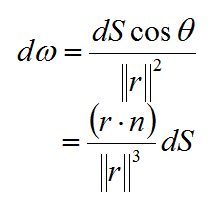
上記式において,球面上にある微小な曲面をとり,その微小面積をdS,rは球の中心から位置ベクトルをrとします。そして,法線ベクトルをnとします。
今実際に考えているのはキューブマップなので,dSは1ピクセル辺りの面積で,rは球の中心から各ピクセルまでの位置ベクトルで,法線ベクトルはキューブの各面の面法線にあたります。
1ピクセル辺りの面積ですが,球を内包するキューブを考えます。単位球の場合は半径1なので,キューブの各辺の長さは2となります。よって,キューブマップの大きさをcube_sizeピクセルとすると,1ピクセル辺りの辺の長さは,( 2.0 / cube_size )となります。したがって,微小面積dSはその2乗値なので,(2.0 * 2.0)/(cube_size * cube_size)となります。次に分子のdot(r , n)ですが,面の法線ベクトルは(1, 0, 0)等のようになり,位置ベクトルの成分も(1, s, t)などのようになるので,内積の値は必ず1となります。
以上より,キューブマップの場合には下記式で立体角が求められます。
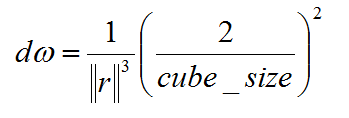
あとは,この立体角を用いて計算すれば近似ができます。
この係数を求める詳しい説明が欲しい方は,
"Stupid Spherical Harmonics(SH) Tricks"とか
"Spherical Harmonics Lighting:The Gritty Details"あたりを読んでください。SH Projectionという単語で検索してもらえれば,その前後に上述した積分形式の式が出てくるはずです。
これで,ようやくSHについても理解が深まりました。あとは,帯域調和関数ですかぁ…時間かかりそうですなぁ
本ソースコードおよびプログラムを使用したことによる如何なる損害も製作者は責任を負いません。
本ソースコードおよびプログラムは自己責任でご使用ください。
プログラムの作成にはMicrosoft Visual Studio 2008 SP1 Professionalを用いています。