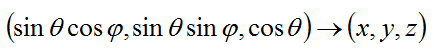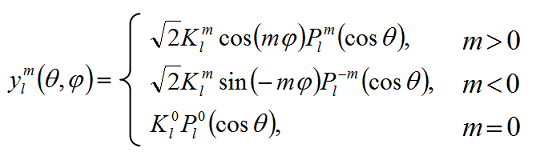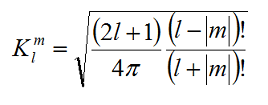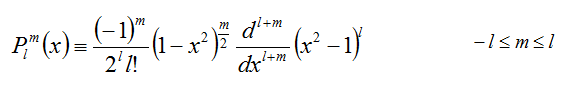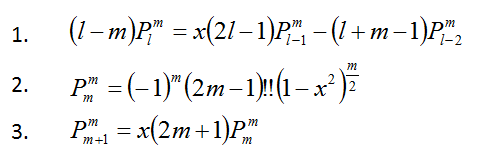球面調和関数(1)

そろそろ，GI系もまともに勉強しなきゃヤヴァイんじゃないかと思ったので，まずはSHからお勉強です。
プログラム的にはXNAで実装したものとほぼ同じものです。

球面調和関数ですが，「いったいこの難しそうな響きの関数は何につかうの？」と思われるでしょう。球面調和関数は，レンダリング方程式を近似して解く際に用いられたりします。
まずはレンダリング方程式から…。
レンダリング方程式は，その名の通りレンダリングを司る方程式です。この方程式は1986にJames Kajiyaによって発表された"The Rendering Equation"という論文に書かれているものだそうです。この論文発表以降，レンダリング方程式の解を正確に近似できるということが，GI(Global Illumiation：大局照明）の定義として用いられるようになったそうです。
GI系の論文を見るとレンダリング方程式がよく出てくるのはそういうわけです。
さて，レンダリング方程式ですが，どういう式かというと下記のようなものになります。



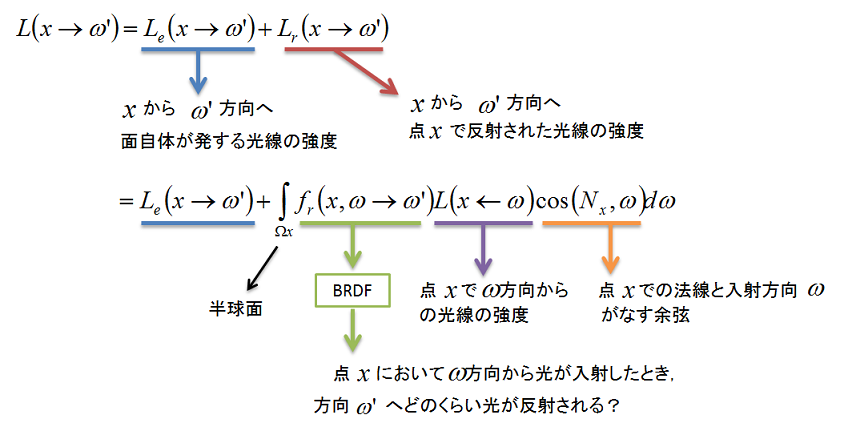
式は「ビジュアルコンピューティング　3次元CGによる画像生成」のp.65から引っ張ってきました。
このレンダリング方程式ですが，何を表しているかというと"物体の表面における光のエネルギーの保存"を表しています。入ってくる光と反射してぶっ飛んでいく光を足したら同じだよってことです。
上の式を見るとわかるように，半球面Ωxで積分が行われます。イメージしやすいように言い換えると，描画するポリゴンの各頂点ごとに，あらゆる方向から入ってくる光に対して一回一回計算を行うイメージです。当然，重たい計算となるので，リアルタイムでくそまじめに解くのは現時点では，難しそうです。そこで登場するのが球面調和関数です。

球面調和関数の数学的な定義についてふれておきます。
球面調和関数は本来，複素数を含む関数なのですがCGの世界では，複素数は考えず実数のみに着目して考えます。CGで一般によくつかわれている球面調和関数は実数球面調和関数です（Real Sphericla Harmonics)が，いちいち実数球面調和関数と言い換えるのも面倒なので，そのまま球面調和関数と呼んでいくことにします。
まず，以下のような座標系を考えます。



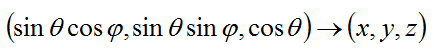
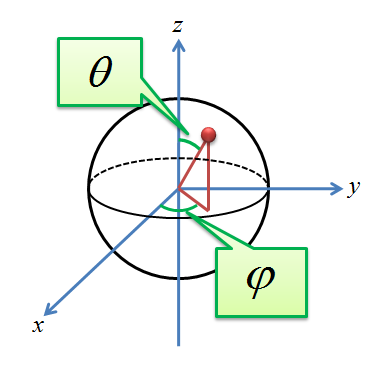
球面調和関数は，慣例的にシンボルyによって表され，その定義は下記のようになります。


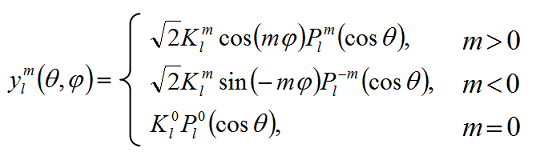
上記式にある，l,mはどの部類に属するかを示すもので，lは正の整数でmは-lから+lまでの整数とします。Kは正規化するための係数で下記式で表されます。


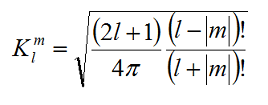
また，式に出てくるPはルジャンドル陪関数（associated Legendre polynomial)と呼ばれるもので，下記のように定義されるそうです。

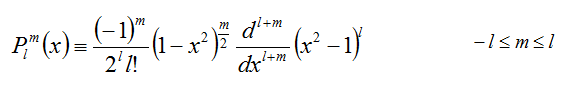
まったくもって，式がよく分からないので"Sphrical Harmonic Lighting: The Gritty and Detail"にこルジャンドル陪関数が漸化式で表されたものが載っていますので，こちらを使うことにします。
ルジャンドル陪関数の漸化式は次のようになります。


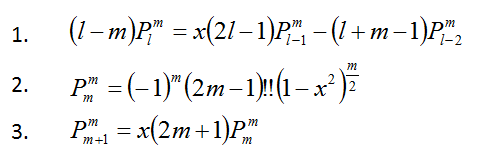
上記2番目に出てくるビックリマーク2つは，2重階乗を意味しています。2重階乗は以下のように2つ飛びで階乗計算を行うものです。


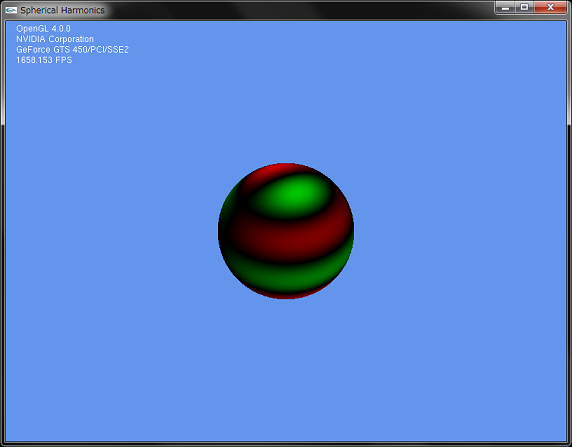
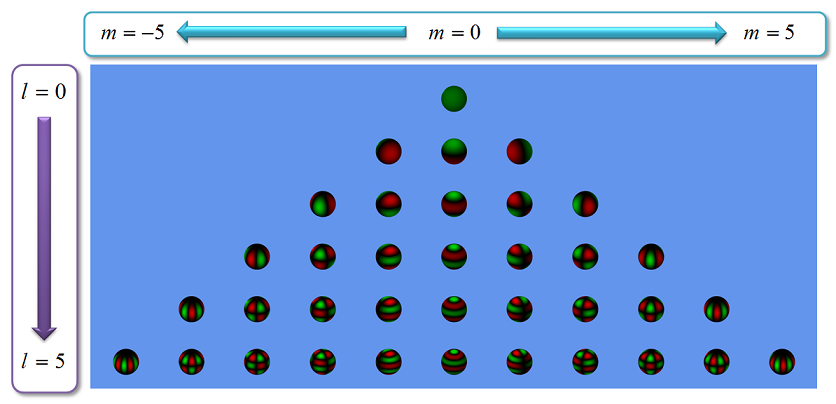
ちなみ，球面調和関数ですが，lとmに値を入れて計算した結果を図示すると下記のようになります。 図において，緑色の部分は計算結果が正の部分で，赤色が負の部分になっています。

とりあえず，球面調和関数にイントロダクションということで，レンダリング方程式の概要と球面調和関数の数学的な定義についてのみ説明してみました。
次は，実際に球面調和関数を用いてキューブマップを近似するプログラムを作ってみようと思います。

本ソースコードおよびプログラムを使用したことによる如何なる損害も製作者は責任を負いません。
本ソースコードおよびプログラムは自己責任でご使用ください。
プログラムの作成にはMicrosoft Visual Studio 2008 SP1 Professionalを用いています。

• SphericalHarmonics.7z (46.4KB)