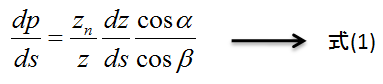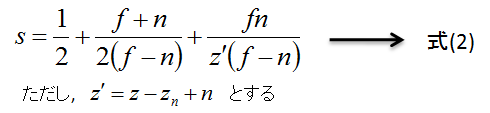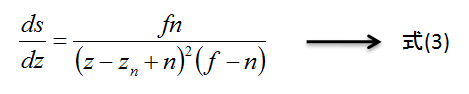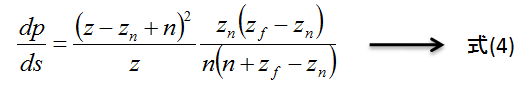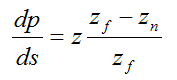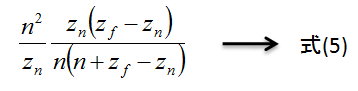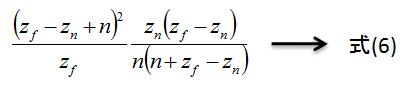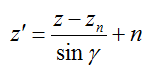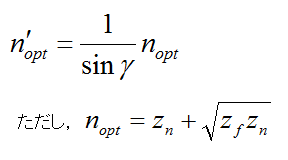Light Space Perspective Shadow Maps
★ 1.はじめに…
ようやくLight Space Perspective Shadow Mapsの実装をしました。
Light Space Perspective Shadow Mapsの論文は
こちらのページからダウンロードできます。
元の論文では、Light Space Perspective Shadow MapsをLiSPSMという風に略していますが、"i"だけ小文字なので何か気持ち悪いので、うちのページではLSPSMと略していくことにします。
画像空間アルゴリズムで問題になるのは、エイリアシングです。もちろん、シャドウマップ技法もその問題を抱えています。このエイリアシングのアーティファクトを低減しようとするいくつかのアプローチがあります。その中で良さそうなアイデアのひとつに透視シャドウマップ(PSM: Perspective Shadow Maps)があります。残念ながら、元々の透視シャドウマップ技法(PSMの論文に書かれている手法)は、いくつか弱点があります。
- ライトが透視変換後の空間へと変換され、頻繁にそのタイプが変化する(点ライトから方向ライト、また向きが逆向きだったり、逆転したライトになっていたり…)。特に、透視変換後の空間を考えるというのは、直感的ではないです。
- 透視変換後の空間はブラックホールを持ち、ブラックホール上に影を投影した際に問題を引き起こしたり、あるいはブラックホールの反対に影を投影するという問題を引き起こします。この問題に対する実用的な解決策は、ブラックホールの前に描画に関係があるオブジェクトを全て含むまで、シャドウマップを生成する際に視点を後ろに移動させることです。ですが、これはシャドウマップのクオリティを下げてしまいます。
- いくつか特殊なケースがあるので、実装が極めて複雑。
- 視点に近いところの影は良いが、遠い所の影はいい加減になりすぎる。
…という感じです。
実際に、前回作ったPSMのサンプルをいじってもらえればわかると思いますが、パラメータ調整とかが面倒なので、使いづらいです。そこで、出てきたのが今回紹介するライト空間透視シャドウマップ技法です。
LSPSMの利点は、ブラックホールに関係がある透視変換は選択されないので、全てのライトを方向ライトとして取り扱い、ライト方向が変化しないという所です。なので、透視シャドウマップの問題の多くはLSPSMによって回避することができます。また、LSPSMはパラメータによって、近いところの影の品質を良くするか、近いところと遠いところのバランスを良くするかなど、ユーザーが調整できることです。さらに、ブラックホールを考えなくて良いので、実装も簡単になります。
ライト空間透視シャドウマップ技法ですが、基本的には透視シャドウマップ技法の最良結果を得られるように、シャドウマップ生成時の座標系を調整するものです。
LSPSMは以下のステップで適用されます。
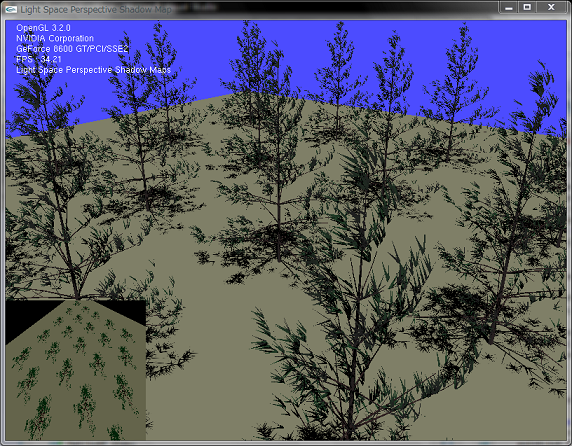
- 視点からの視錘台と影生成元になりうる全てのオブジェクトを捉え、凸体(Convex Body)Bとする。
- シャドウマップに平行な視線ベクトルを持つ、適切な透視錘台(Perspective Frustum)PでBをエンクローズする。
- 錘台P上の透視参照点pから近平面までの距離nを調整することによって、歪み効果の強さを制御する。
- 普通のシャドウマップと同じように、シャドウマップを生成時・描画時の両方の間、Pを適用する。
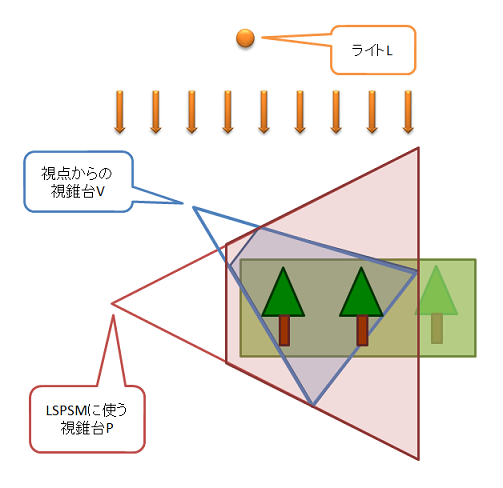
まずは、凸体Bを求めます。Bですが、構成するためには視点からの視錐台を含んでいる必要があります。次に、この視点から視錐台を構成する8つの点以外に、視錐台中に影を落とすオブジェクトがあるかどうかを調べます。判定の結果、影を落とす可能性がある場合には、Bにこのオブジェクトの頂点を追加します。頂点を追加するといっても、オブジェクトのAABB(Axis Aligned Bounding Box)を作成して追加…ということになります。
凸体を求めるために、視点からの視錐台を求めます。
今回視錐台は、(-1, -1, -1)〜(1, 1, 1)で構成される立方体に、ビュー射影行列の逆行列を掛けることによって求めています。コードにすると以下のような感じになります。
00030: //-----------------------------------------------------------------------
00031: // Name : ComputeViewFrustum()
00032: // Desc : カメラの視錐台を求める
00033: //-----------------------------------------------------------------------
00034: PointList ComputeViewFrustum(const MATRIX viewProj )
00035: {
00036: PointList result;
00037: result.Clear();
00038:
00039: // 立方体を作成
00040: VECTOR3 v[8];
00041: v[0] = VECTOR3( -1.0f, +1.0f, -1.0f );
00042: v[1] = VECTOR3( -1.0f, -1.0f, -1.0f );
00043: v[2] = VECTOR3( +1.0f, -1.0f, -1.0f );
00044: v[3] = VECTOR3( +1.0f, +1.0f, -1.0f );
00045: v[4] = VECTOR3( -1.0f, +1.0f, +1.0f );
00046: v[5] = VECTOR3( -1.0f, -1.0f, +1.0f );
00047: v[6] = VECTOR3( +1.0f, -1.0f, +1.0f );
00048: v[7] = VECTOR3( +1.0f, +1.0f, +1.0f );
00049: for( int i=0; i<8; i++ )
00050: {
00051: result.Add( v[i] );
00052: }
00053:
00054: // ビュー行列→射影行列の逆変換を行う行列を求める
00055: MATRIX invViewProj = Invert( viewProj );
00056:
00057: // 立方体に逆変換する行列をかけ、視錐台を求める
00058: result.Transform( invViewProj );
00059:
00060: return result;
00061: }
次は、視錐台中に影を落とすオブジェクトがあるかどうかの判定です。
方法ですが、各オブジェクトのAABB(Axis Aligned Bounding Box)を作成して、各オブジェクトのAABBをマージさせてシーンを構成する1つのAABBを作成し、AABBの各頂点からライトベクトルの方向に光線を飛ばして、その光線が視錐台を構成する6つの平面と交差するかどうかの判定を行えば良いと思います。DirectXを使っている方であれば、D3DXPlaneIntersectLine()関数とかD3DXの算術関数を使って簡単に実装できると思います。うちはOpenGLで、便利関数ないので今回は実装していません。
透視変換のための錐台Pをライト空間で求めます。
ライト空間は以下の方法で構築します(下図参照)
・y軸→ライトベクトルlによって定義されます。(下図では、y軸はライトに向かう方向を示しています)
・z軸→ライトベクトルに垂直で、カメラの視線ベクトルvを含む平面上。
・x軸→直交座標系を形成するように定める。
ちなみに、下の図なんですが左手座標系になっています。OpenGLは右手座標系なので注意してください。
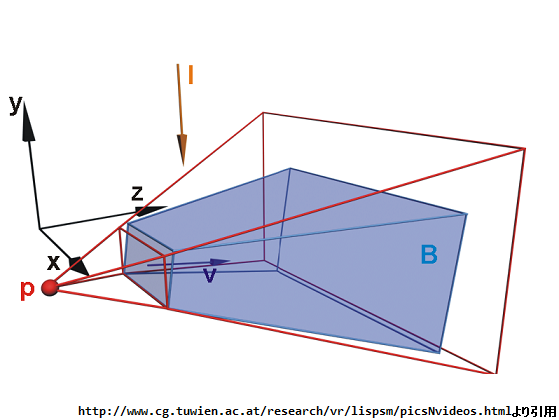
まず、y軸ですがこれはそのままなので、問題ないですね。続いてz軸ですが、ライトベクトルに垂直かつカメラの視線ベクトルを含む平面上と言っているので、ライトベクトルとカメラの視線ベクトルの外積を求めれば出ます。最後のx軸ですが、2つの軸が求まれば自動的に決まるので、特別に考えなきゃいけないことはないです。
さて、ライト空間の構築がこれで出来ました。いよいよ透視錐台Pを求めます。まず、凸体Bを構成する頂点群をライトのビュー行列を用いてライト空間に変換します。続いて、変換した頂点群からAABBを求めます。今は、ライト空間でものごとを考えているので、求めたAABBのy方向の長さd(=abs( max.y - min.y ))がPの近平面から遠平面までの距離になります。近平面から遠平面までの距離dが求まっているので、近平面までの距離nが求まれば、遠平面までの距離は n + d とすぐに求めることができます。では、nはどうやって決めるの?ということが、特別に「こう決めなきゃいけない!」というものはないようです。
パラメータnですが、このnの値によってシャドウマップの歪み方に影響がでます。nの値をPの近平面に近い値を選択すれば、オリジナルの透視シャドウマップに近い効果になり、遠平面より遠く離れるような値を選択した場合には、透視の効果が軽くなり、通常のシャドウマップにに近い効果になります。そこで、真ん中ぐらいのちょうどバランスのいい値にしてやれば、透視シャドウマップみたいに遠くが雑にならないし、通常のシャドウマップよりは品質のいい影がつくれるんじゃない?ということで、最適なパラメータnの決め方が論文に載っています。
最適なパラメータnを求め方を見ていく前に、もう一度透視エイリアシングについて復習しておきます。ちなみに、これから述べる話は、視線の方向がライトの方向に垂直である理想的な場合として扱うので注意してください。
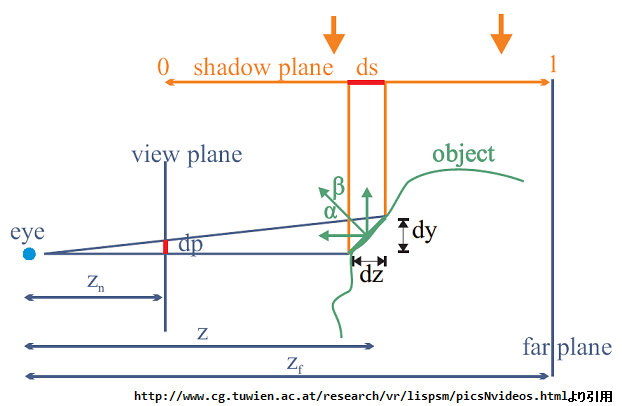
上図のようにz, zn, dz, ds, α, βを定めた時のシャドウマップのエイリアシングエラー(dp/ds)は以下の式で求められます。
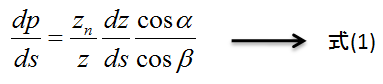
透視シャドウマップ系であつかうのは、((1/z) * (dz/ds))部分の透視エイリアシングでした。通常のシャドウマップでは,歪みは出ないため(dz/ds)は一定です。上図を見てもらえればわかるのですが、zを大きくすると(1/z)が0に近づくため、エラーは小さくなります。逆にzの値を小さくすると、(1/z)の値が大きくなるので、エラーも大きくなります。
ここで、(dp/ds)を分析するために、シャドウマップのパラメータs=s(z)を考えてみます。例えばOpenGLのglFrustum()で考えてみると…
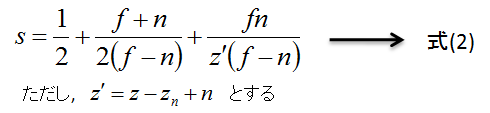
…となるそうです。
式(2)をzで微分すると次式になります。
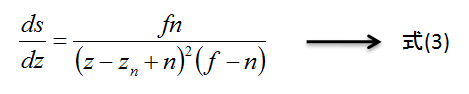
ここで、投影エイリアシング(=cosα/cosβ)を1とし、式(1)に代入すると次式が得られます。
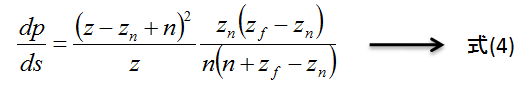
この式(4)を使って、nによるシャドウマップのエラーを考えていきます。
まず、nを無限大に近づけてみます。

nを無限大に近づけると、通常のシャドウマップに一致しzに反比例する式になります。
次に、n=znを代入すると、次のようになります。
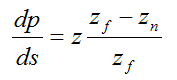
上式をみるとわかるように、zに比例する式となります。
ここでもう一度、式(1)を見てみましょう。シャドウマップのエラーはzの値によって、変化します。シャドウマップのzの範囲は[zn, zf]です。そのため、エラーがもっとも小さくなるのはz=zfのときです。一方エラーが大きくなるのは、z=znのときです。先程までnについて式(4)に値を代入し調べましたが、nの値によって反比例する場合と比例する場合できてます。よってzが大きいとマズイ場合、zが小さいとマズイ場合が出てきます。そこで、マズイ場合を避けるためにz=zfのときと、z=znのときにエラーが同じになるようなnを求めておけば、うまく対応できそうです。
そんなわけで求めてみます。式(4)にz=znを代入すると次式が得られます。
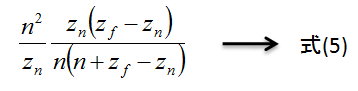
続いて、式(4)にz=zfを代入し、次式が得られます。
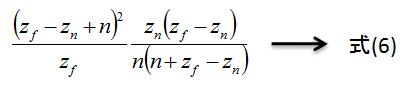
式(5)と式(6)が等しくなるようなnを求めたいので、等号でつなぎ、nについて求めます。

これで、一応論文にのっているnoptが求められました。
視線の方向がライトの方向に垂直である理想的な場合について説明してきました。しかし、実際にはカメラをルックアップ・ルックダウンさせるケースもあるので、垂直になるのはまれかもしれません。論文でも触れられていますが、ライトの方向と視線の方が平行である場合には、シャドウマップの品質を向上させるパラメータ化はないそうなので、平行である場合には、通常のシャドウマップに切り替えて使用します。また、一般的な場合に視空間のz座標はライト空間のz座標にあんまり一致しないようです。そこで、チルト角を考慮した最適なパラメータnを考える必要があります。そこで、式(2)のz'を次式に置き換えて、nを求めます。
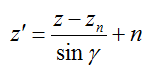
ちなみに視線ベクトルとライトベクトルのなす角γですが、下図を参照してください。
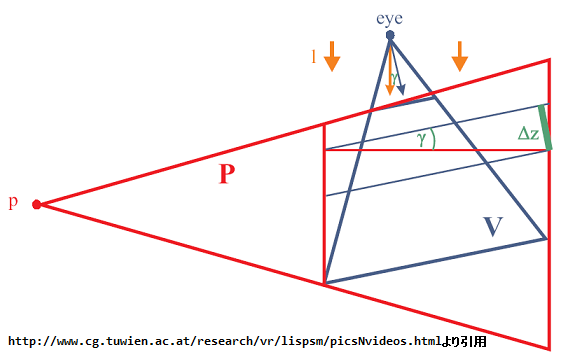
z'を置き換えて求めた最適なパラメータnは次式になるそうです。(ちなみに、この式の導出はチェックしていないっす。)
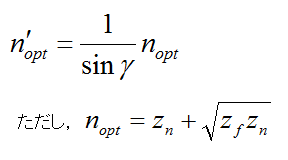
そんなわけで、nopt'を用いて透視錐台Pを作成します。
後は、求めたPを使ってシャドウマップの生成と、深度比較を行えばライト空間透視シャドウマップになります。
さて、実装ですが以下のような感じです。
00182: //------------------------------------------------------------------------
00183: // Name : ComputeMatrix_LSPSM()
00184: // Desc : ライト空間透視シャドウマップ行列を計算
00185: //------------------------------------------------------------------------
00186: void LSPSMCalculator::ComputeMatrix_LSPSM()
00187: {
00188: VECTOR3 max, min;
00189:
00190: //視線ベクトルとライトベクトルのなす角度を求める
00191: float angle = GetCrossingAngle(viewDirection, lightDirection);
00192:
00193: //なす角が0度または180度の場合
00194: if ( angle == 0.0f || angle == Pif )
00195: {
00196: //ライトによる歪みがないので通常のシャドウマップを適用
00197: ComputeMatrix_USM();
00198: return;
00199: }
00200:
00201: //リストをコピーしておく
00202: PointList listClone = pointList;
00203:
00204: float sinGamma = sqrtf( 1.0f - angle * angle );
00205:
00206: // アップベクトルを算出
00207: VECTOR3 up = ComputeUpVector( viewDirection, lightDirection );
00208:
00209: //ライトのビュー行列を求める
00210: lightView = CreateLookAt( eyePosition, (eyePosition + lightDirection), up );
00211:
00212: //ライトのビュー行列でリストを変換し、AABBを算出
00213: pointList.Transform( lightView );
00214: pointList.ComputeBoundingBox( min, max );
00215:
00216: //新しい視錐台を求める
00217: const float factor = 1.0f / sinGamma;
00218: const float z_n = factor * nearClip;
00219: const float d = abs( max.y - min.y );
00220: #if NEW_FORMULA
00221: // New Formula written in ShaderX4
00222: const float z0 = - z_n;
00223: const float z1 = - ( z_n + d * sinGamma );
00224: const float n = d / ( sqrtf( z1 / z0 ) - 1.0f );
00225: #else
00226: // Old Formula written in papers
00227: const float z_f = z_n + d * sinGamma;
00228: const float n = ( z_n + sqrtf( z_f * z_n ) ) * factor;
00229: #endif
00230: const float f = n + d;
00231: VECTOR3 pos = eyePosition - up * ( n - nearClip );
00232:
00233: //シャドウマップ生成用ライトのビュー行列
00234: lightView = CreateLookAt( pos, (pos + lightDirection), up );
00235:
00236: //Y方向への射影行列を取得
00237: MATRIX proj = GetPerspective( n, f );
00238:
00239: //透視変換後の空間へ変換する
00240: Multiply( lightView, proj, lightProjection );
00241: listClone.Transform( lightProjection );
00242:
00243: //AABBを算出
00244: listClone.ComputeBoundingBox( min, max );
00245:
00246: //範囲を適正にする
00247: MATRIX clip = GetUnitCubeClipMatrix( min, max );
00248:
00249: //シャドウマップ生成用ライトの射影行列を求める
00250: Multiply( proj, clip, lightProjection );
00251: }
論文の著者のサンプルプログラムを参考したので、まんまって感じですね。それを堂々とのけるのもどうかと思ったんですが、載せちゃいます。
ちなみに#ifで区切っている部分ですが、ShaderX4をみると新しい式として載っていたので使ってみました。説明がさらっと終わってしまっていて、どっからどう出したのか良くわかんないです。
せっかくなので、比較してみました。
まずは、4096x4096です。
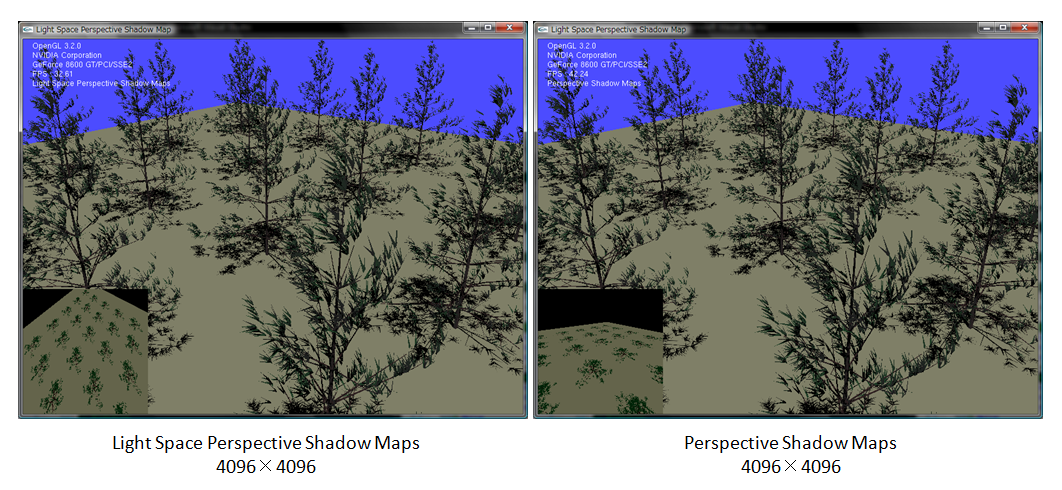
ほとんどわからないですが、一番奥の木の影の大きさが違っています。PSMの方が手前側が綺麗です。
解像度を減らしていってみます。続いて2048x2048です。
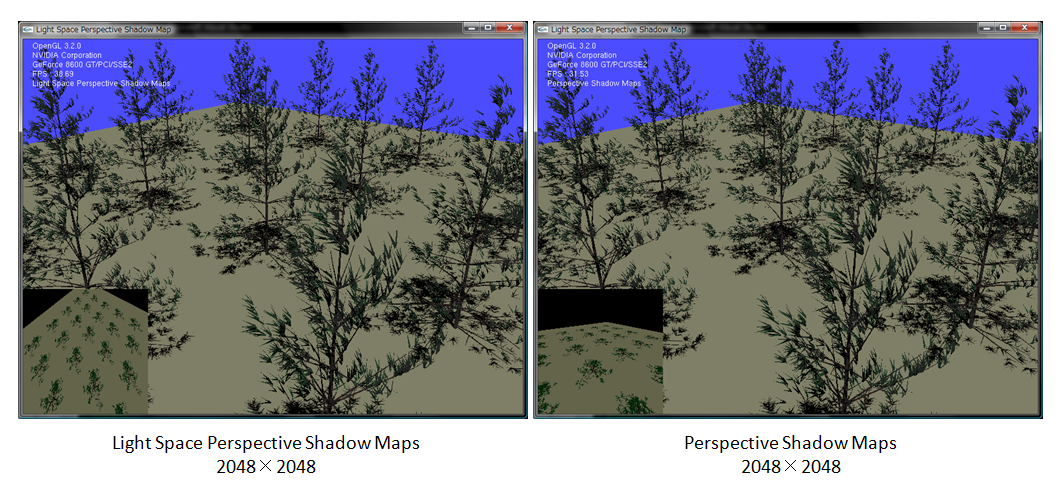
まだPSMの方が綺麗に見えます。
さらに減らします。1024x1024です。
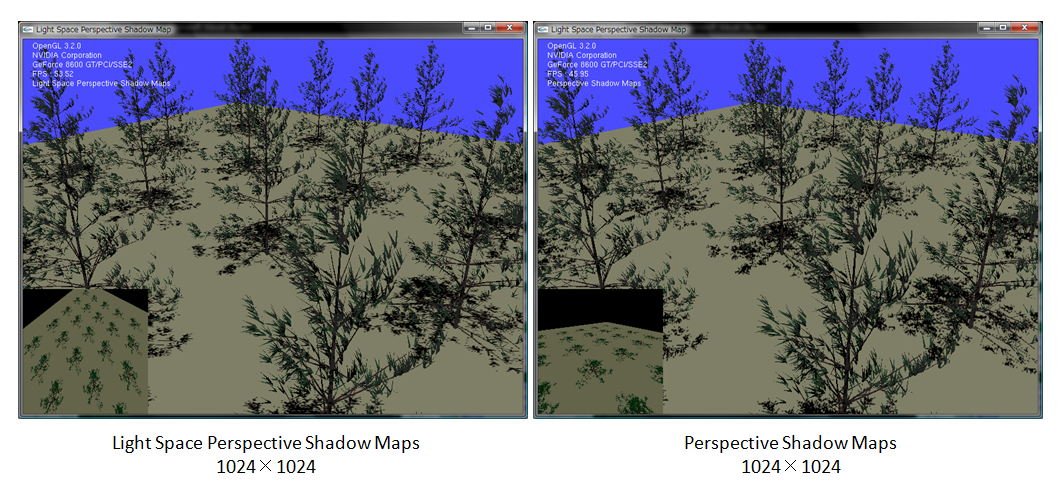
ここまでくるとPSMの影が大雑把になってきたかな〜って感じですかね?
さらに減らしてみましょう。512x512です。
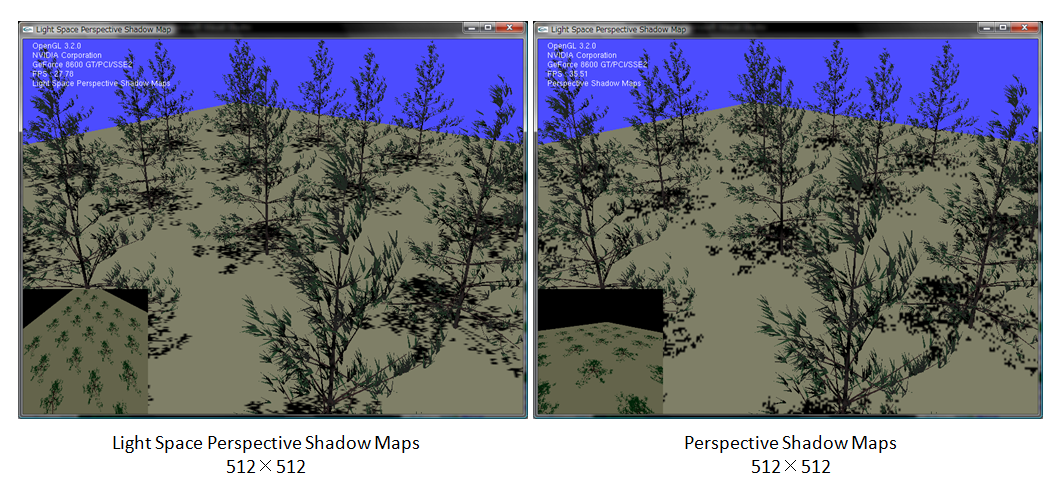
この辺りまで減らすと、LSPSMの方が綺麗に見えて、PSMの方が大雑把に見えます。
さらに×2、減らしてみましょう。256×256です。

PSMの方は一番奥の木の影が若干なくなってきています。やはりLSPSMの方が見た目が良い感じがします。
もっと減らしましょう。128×128です。
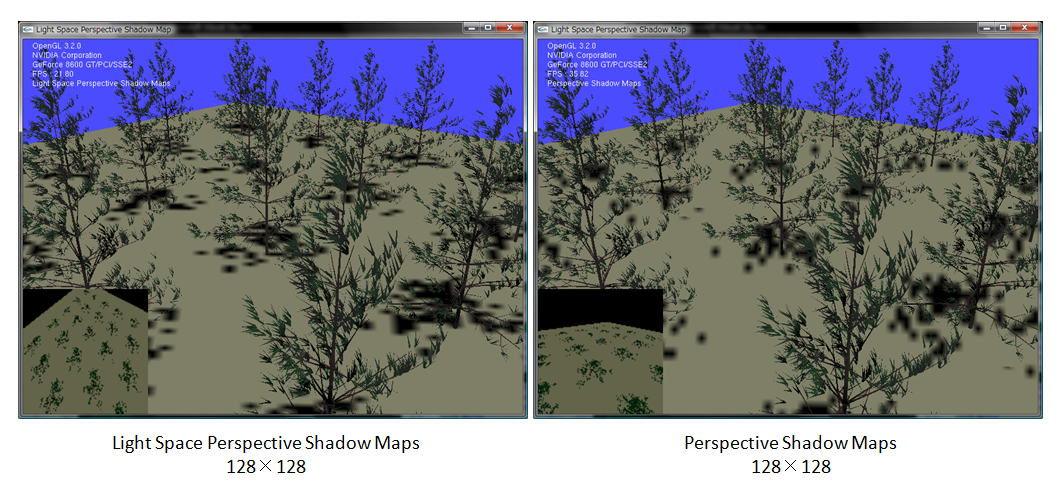
128あたりまでくると、PSMの一番奥の木の影はなくなってしまっていますね。
もっと減らしてみます。64×64です。
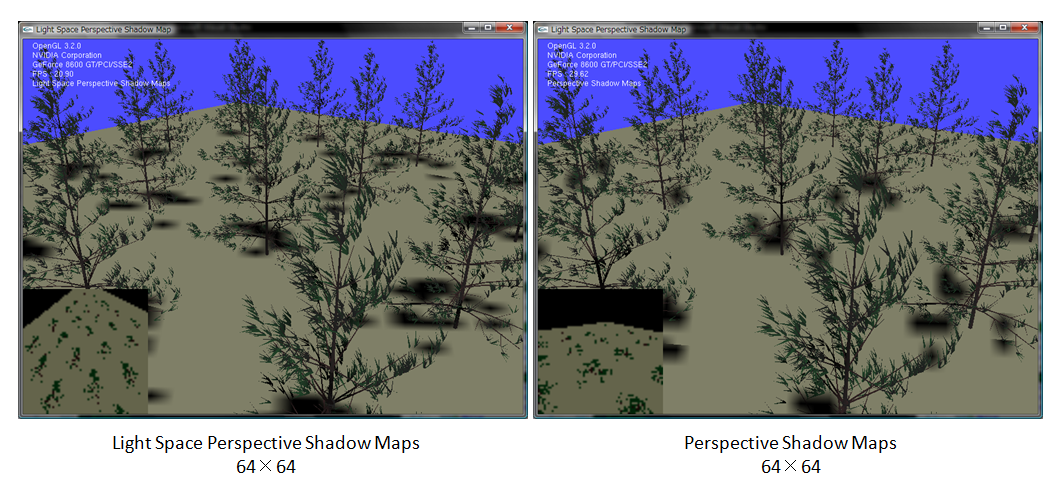
LSPSMの方が見た目が良いですね。
最後、32×32を見てみましょう。
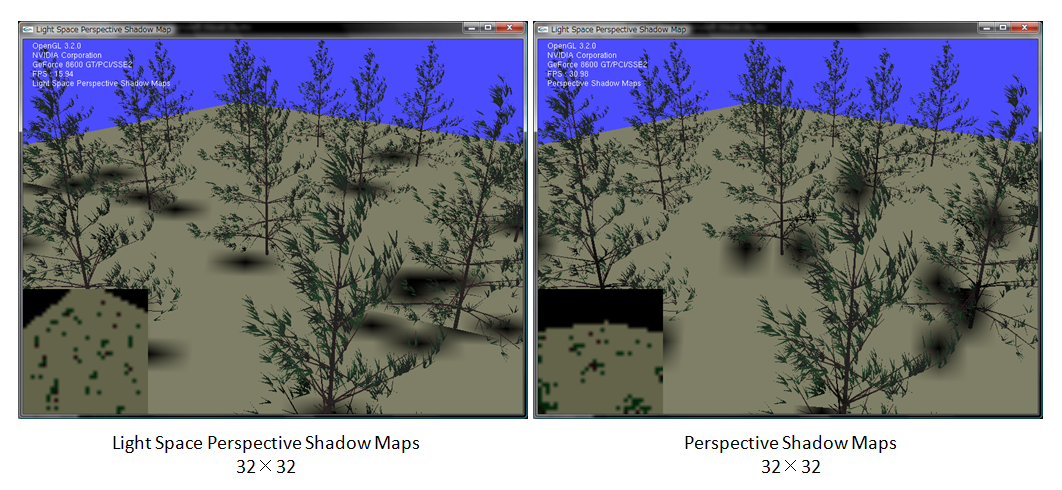
五十歩百歩のような気もしますが、影の数でいくとLSPSMの方が良さそうです。
個人的な感想ですが、めちゃくちゃ高解像度が使える場合はPSM、それ以外はLSPSMにしておいた方がいいんじゃないかと思います。
ようやくトラウマになっていたLSPSMの実装ができました。ずっと、うまくいかなくて悩んでいたんですよね〜。これで色々とスッキリしたので、そろそろゲーム開発の方にも手を出してみようかと思います。
本ソースコードおよびプログラムを使用したことによる如何なる損害も製作者は責任を負いません。
本ソースコードおよびプログラムは自己責任でご使用ください。
プログラムの作成にはMicrosoft Visual Studio 2008 SP1 Professional, Cg Toolkit 2.2を用いています。