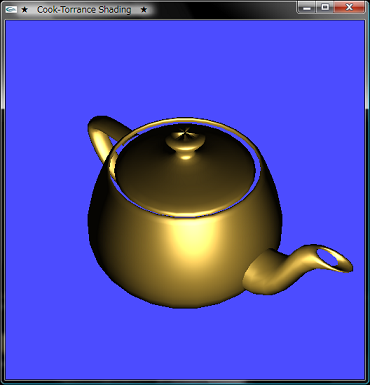
下の画像が実行結果なんですけど,金属っぽくみえますかね?

ライティング(4) Cook-Torrance★ 1.はじめに…
今回は金属の反射モデルに適しているとされるCook-Torranceをやります。
下の画像が実行結果なんですけど,金属っぽくみえますかね?  ★ 2.Cook-Torranceモデル
Cook-TorranceモデルはPhongモデルよりもより精密なモデルとして,反射率は波長および入射角に依存することも考慮し,反射率はフレネル(Fresnel)の式を用いています。
Cook-Torranceの鏡面反射モデルからの鏡面反射色は次式のようになります。 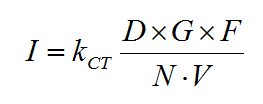 ただし,kctは色のスペクトルに依存する反射率,Dはマイクロファセットの分布関数,Gは幾何減衰率,Fはフレネルの公式による反射係数,Nは物体表面の法線ベクトル,Vは視線ベクトルを表します。 また分数式の分子にある×記号は外積ではなく単なる乗算です。 式で出てきたマイクロファセットの分布関数Dは 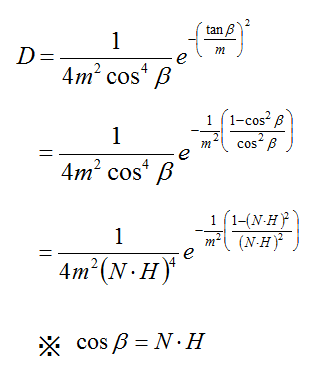 です。 パラメータとして用いている角度βは,面の基準となる法線ベクトルと,ハーフベクトルの間の角度です。 マイクロファセットの分布関数でもう1つあるパラメータmは面の粗さを決める適当な定数だそうです。このmの値が小さいほどシャープンな分布になるそうです。 あと鏡面反射色の式で出てくる幾何減衰率Gは次の式になるそうです。 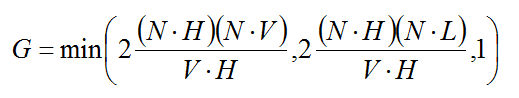 Gはminの3つの引数のなかで最小の値を用いるそうです。 鏡面反射色の式で出てくるフレネル項Fはフレネルの公式によって求めます。 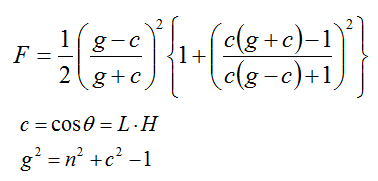 残りの鏡面反射色の式の分母の(N・V)の項は観測者から見た単位面積あたりのマイクロファセットの濃度になるそうです。 あとは式をコードに落としましょう。 PhongのプログラムとCook-Torranceは鏡面反射の項が違うだけなので,ピクセルシェーダの部分のみ書き換えます。 分ける必要はないのですが,わけといた方が見やすいので,Beckmann分布を求める関数とフレネル項を求める関数を作っておきます。
37 : //----------------------------------------------------------------------------------
38 : // Name : CalculateBeckmann()
39 : // Desc : Beckmann分布関数の計算
40 : //----------------------------------------------------------------------------------
41 : float CalculateBeckmann(float m, float cosbeta)
42 : {
43 : return (
44 : exp(-(1-(cosbeta*cosbeta))/(m*m*cosbeta*cosbeta))
45 : /(4*m*m*cosbeta*cosbeta*cosbeta*cosbeta)
46 : );
47 : }
48 :
49 : //----------------------------------------------------------------------------------
50 : // Name : CalculateFresnelTerm()
51 : // Desc : フレネル項の計算
52 : //----------------------------------------------------------------------------------
53 : float CalculateFresnelTerm(float n, float c)
54 : {
55 : float g = sqrt(n*n + c*c - 1);
56 : float T1 = ((g-c)*(g-c))/((g+c)*(g+c));
57 : float T2 = 1 + ( (c*(g+c)-1)*(c*(g+c)-1) )/( (c*(g-c)+1)*(c*(g-c)+1) );
58 : return 0.5 * T1 * T2;
59 : }
60 :
あとはピクセルシェーダの部分を直します。
81 : //
82 : // Pixel Shader
83 : //
84 : float4 CookTorrancePS(VertexOutput input) : COLOR
85 : {
86 : float3 L = normalize(lightPosition - input.objPosition); // ライトベクトル
87 : float3 N = normalize(input.normal); // 法線ベクトル
88 : float3 V = normalize(eyePosition - input.objPosition); // 視線ベクトル
89 : float3 H = normalize(L + V); // ハーフベクトル
90 :
91 : // 計算に使う角度
92 : float NV = dot(N, V);
93 : float NH = dot(N, H);
94 : float VH = dot(V, H);
95 : float NL = dot(N, L);
96 :
97 : // Beckmann分布関数
98 : float D = CalculateBeckmann(0.35f, NH);
99 :
100 : // 幾何減衰率
101 : float G = min(1, min(2*NH*NV/VH, 2*NH*NL/VH));
102 :
103 : // フレネル項
104 : float F = CalculateFresnelTerm(20.0f, dot(L, H));
105 :
106 : // 拡散反射光・鏡面反射光
107 : float3 diffuse = lightColor*Kd*max(dot(L, N), 0);
108 : float3 specular = lightColor*Ks*max(0, F*D*G/NV);
109 :
110 : return float4(input.color + diffuse + specular, 1.0f);
111 : }
112 :
input.colorにはVertex Shaderで計算した環境光の値が入ってくるようになっています。★ Download
本ソースコードおよびプログラムを使用したことによる如何なる損害も製作者は責任を負いません。
本ソースコードおよびプログラムは自己責任でご使用ください。 プログラムの作成にはMicrosoft Visual Studio 2005 SP1 Professional, Cg Toolkit 2.0 Decemberを用いています。 |